This page gives detailed descriptions of the Sun/Moon Calculator features. An illustrative introduction to many of these features is given in the Sun/Moon Calculator tutorial.
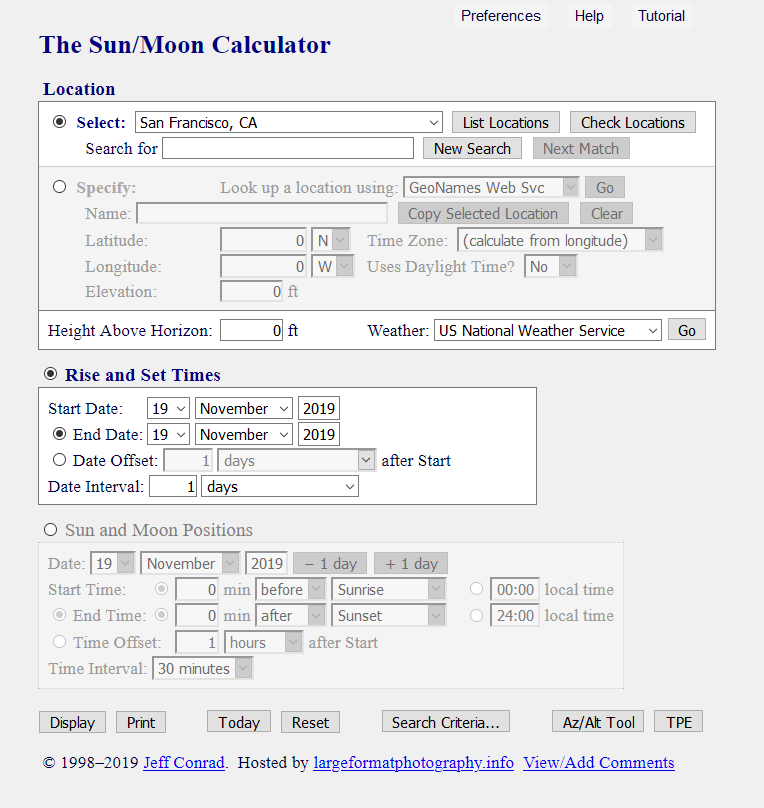
The Sun/Moon Calculator opens with the main form displayed, as shown in
Figure 1.

Figure 1. Calculator Main Form
The main form is divided into several areas.
The location can be set in one of several ways:
The calculator can show Sun and Moon rise and set times for a specified range of dates. Criteria such as ranges of azimuth, altitude, and phase can be given to find dates on which the Sun or Moon rises or sets near a natural or man-made landmark; this capability is arguably the calculator’s most useful feature. This area is covered under Rise and Set Times.
Sun and Moon positions can be shown at various times during day. The start and end times can be given directly, or they can be given relative to a Sun or Moon event such as rise or set. See Sun and Moon Positions for more information.
Buttons at the bottom of the form display Sun and Moon rise and set times or positions, set the current date or reset all values to default, or run other applications that can help plan a shot. They are described in detail in the section Bottom-of-Form Buttons.
Check Select: to choose a location from the calculator’s database, or Specify: to search for a location in an online database or enter location properties manually. Values entered under Specify are ignored unless the Specify: radio button is checked.
Search the locations database for a location that matches the specified pattern; the location matches if any part of its name contains the pattern. For example, ban will match Fairbanks, AK and several others as well as Banff NP, AB and Bangkok, Thailand. Entering a few additional characters will usually give a unique match: banf will match only Banff, and bangk will match only Bangkok.
By default, the pattern is simple text; there are no wildcards or boolean operators. The search is case sensitive if the pattern contains any uppercase letters, including a regular expression such as [A-K]; otherwise, case is ignored. For example, Ban will match Banff and Daka, Bangladesh but not Fairbanks, AK or Albany, NY. All entries are stored as ASCII text, so the pattern should not contain accented characters; to match Orléans, France, enter Orleans, F.
A search is performed as each character is entered; the selected location updates to the first matching location. The selected location also updates as the Backspace key is pressed. Pressing Enter or clicking Next Match searches for the next matching location. For example, entering NY and pressing Enter several times will find all locations in the state of New York; observing capitalization prevents unwanted matches. If no location matches the pattern, the selected location is not updated; an error message is given, and the character that caused the match to fail is erased.
When the location search feature is enabled, the following buttons are displayed:
If Allow regular expressions in location searches on the User Preferences form is checked, the pattern can include JavaScript regular expressions; for example, NP.*UT can be used to find all National Parks in Utah.
The location search feature is available only if Show location search on the User Preferences form is checked; it is enabled by default.
Results are written to the console, so you’ll need to open a browser web console to see them.
If your location is not in the internal database, you can specify its properties. In most cases, though, the “specification” can be done automatically by a Web service that will fill in the calculator’s form fields if it finds a location that matches your query.
Automatic Fill-In
Several online services—
Because of the automatic fill-in, using one of these services is
usually the easiest way to look up and enter a location.
The search syntax differs from that used for the
calculator’s built-in database; in particular, all
searches are case insensitive, and regular expressions are not
allowed. The syntax varies slightly among the different
services; the differences are explained in the descriptions that
follow.
GeoNames Web Services use a worldwide database that includes
latitude, longitude, elevation, and time zone for named
features. The USGS searches include only locations for the
United States and its territories; they use the GeoNames service
to obtain time zone information. For locations in the US, all
three services usually give essentially the same results.
Having multiple options is nonetheless handy if one of the
services is slow or down altogether.
GeoNames Web Svc uses the GeoNames database
mentioned above; the database includes many natural features as
well as populated places. For US locations, the data generally
seem to match those of the USGS GNIS.
The search syntax is somewhat different from that for searching
the built-in location database. The search is always case
insensitive, so that San francisco (which will fail
when searching the internal location database) will work just
fine. Regular expressions are not allowed.
By default, a location name without a comma (e.g.,
chicago) must exactly match the feature name; if an
asterisk (“*”) is prepended to the location name
(e.g., *chicago), the name need only match part of
the feature name, so this entry will match North Chicago and
Chicago Heights. The name must still consist only of one or
more whole words, however, so that *chicag will not
work.
If an asterisk (“*”) is appended to the location name
(e.g., chicago*), the search will match all locations
that begin with the specified name (e.g., Chicago
Trail). For compatibility with regular expressions, prepending
a caret (“^”) will have the same effect.
The asterisk is not a true wildcard, however—
If the name includes a comma, the text before the comma is the
location name, and the text after the comma is one or more
additional characteristics of the location (e.g., the country,
state, or province, or other characteristic such as feature
type) described on the GeoNames
search page.
For example, a search for Durango will produce a
large number of matches, whereas a search for Durango,
CO will produce only a few. A search for Durango,
ppl will match only populated places.
In addition, the name can include the postal abbreviation for a
Canadian province (e.g., Vancouver, BC).
Text after the comma can match more than one parameter (e.g.,
CA will match the state code for california
but will also match the country code for Canada, so a search for
mount williamson,ca will match Mount
Williamson in British Columbia as well as Mount Williamson in
California. Similarly, mt will match
features that are mountains, but will also match the state code
for Montana.
The space between the comma and the first text is optional, as
indicated in the last example above.
Regardless of the format of the query, the name of a matching or
selected location is entered into the Sun/Moon Calculator in the
same format as used in the internal location database:
name, country, or for a
location in the United States or Canada as name, state or name,
province, using the postal abbreviation for the
state or province.
The results from the basic GeoNames search do not always include
a location’s elevation; consequently, when there is more
than one matching location, some of the locations in the list
may not show the elevation. Once a location is selected,
however, the elevation is usually found from an additional
query, although this can sometimes result in a slight delay for
the elevation to be filled in on the calculator form.
In some cases, a country may be known by more than one name
(e.g., Myanmar was previously Burma, the name still used by the
US Department of State). The GeoNames service returns a country name of
Myanmar [Burma]; because the Sun/Moon
Calculator only allows a single name (and does not allow
punctuation other than a hyphen), the result of the query must
be edited to choose one name or the other.
If the location name is blank, GeoNames Web Svc
will open the interactive GeoNames page, which functions
similarly to those of the other sources. Latitude and longitude
are shown as N|S|E|W dd°
mm′ ss″.
The calculator uses the free GeoNames Web service, and the
servers on which it relies are sometimes heavily loaded or
unavailable altogether. If the service does not respond in 16
seconds, the request times out and a message is given to that
effect. A single timeout may arise simply because the servers
are heavily loaded, but several in succession usually mean that
the servers are down. If that happens, you can try one of the
USGS services, clear the location name and perform a search
using the interactive GeoNames Web page, or choose another
database.
USGS GNIS XML Svc
searches the USGS Geographic Names Information System database
maintained by the US Board
on Geographic Names.
By default, the search only finds locations that exactly match
the specified name (because of the way database records are
managed, there sometimes are matches to other locations).
If an asterisk (“*”) is appended to the location
name (e.g., chicago*), the search will match all
locations that begin with specified name (e.g., Chicago Trail);
for compatibility with regular expressions, prepending a caret
(“^”) will have the same effect. Prepending an
asterisk has no effect; the location must still match the
beginning of the specified name. As with the GeoNames search,
the asterisk is not a true wildcard; using it other than at the
beginning or end of the search pattern will usually cause the
search to fail.
A US state can be specified by appending a comma and either the
state’s full name or its two-character postal code; the
spelling of either must be exact, though case does not matter.
The results from the search do not always include
a location’s elevation; consequently, when there is more
than one matching location, some of the locations in the list
may not show the elevation. Once a location is selected,
however, the elevation is usually found from an additional
query of the GeoNames database, although this can sometimes
result in a slight delay for the elevation to be filled in on
the calculator form. The time zone information is always found
using the GeoNames database.
If the location name is blank, USGS GNIS XML
Svc will open the interactive
USGS GNIS page, described below.
USGS TX Water Sci uses a search provided by
USGS Texas Water Science Center. It queries much the same
information as the USGS GNIS XML
Service described above, but the search syntax is somewhat
different. By default, the search will find any location whose
name begins with the name specified, but an exact match to the
entire name is not required, so a search for chicago
will yield many results. For compatibility with the other
lookup services, a prepended caret (“^”) is
accepted but has no effect. An asterisk
(“*”) can be used as a wildcard anywhere
in the name given; the asterisk will match any sequence of
characters, *chicago will match all locations whose
names include “chicago”, and *chic*o will
match many additional locations. It is not possible to require
an exact match; the search always behaves as if an asterisk had
been appended to the pattern, so chicago has the same
effect as chicago*.
A US state can be specified by appending a comma and either the
state’s full name or its two-character postal code; the
spelling of either must be exact, though case does not matter.
The search uses the GeoNames database to obtain the time zone,
and the elevation if it is not included in the GNIS record.
Lookup Only
USGS GNIS (USA)
uses an interactive form for querying the USGS Geographic
Names Information System, which is arguably the most
authoritative source for places in the United States. With the
default search, latitude and longitude are shown in USGS packed
DMS format ([d]ddmmssN|S|E|W). The values may be
copied and pasted into the relevant fields of the Sun/Moon
Calculator; the hemisphere indicator (N or
S, E or W) on the calculator form is set to match the
pasted value. With the Advanced Search, coordinates can be
displayed either as packed DMS or decimal. With the latter
format, ensure that the hemisphere indicator is N or E when pasting a
positive latitude or longitude; although a negative value is
always taken as a south latitude or west longitude, the
interpretation of a positive value is determined by the
hemisphere indicator.
Unlike the interface through the Sun/Moon Calculator described
above, searches here use only plain text.
GeoNames uses an interactive interface to
the GeoNames geographical database described above; basic and advanced
searches are available. Unlike the interface through the
Sun/Moon Calculator described above, searches here use only
plain text.
NGA GEOnet
The U.S. National Geospatial-Intelligence Agency’s
GEOnet
Names Server is useful for locations outside the United
States (in most cases, click on the “GNS Search - Text
Based” link at the top of the left frame). Clicking on
the value in the Latitude/Longitude column toggles the format
between DMS (shown as dd°
mm′ ss″ N|S|E|W) and decimal;
when copying and pasting a positive decimal latitude or
longitude, ensure that the hemisphere indicator is set to N or E.
Getty Thesaurus uses the
Getty Thesaurus of Geographic Names and is useful for many
places worldwide. Latitude and longitude are given in both DMS
and decimal formats; either format may be copied and pasted into
the Sun/Moon Calculator. If the DMS format (including the
hemisphere indicator) is pasted into the form, the hemisphere
indicator on the form is automatically set; when pasting a
positive decimal latitude or longitude, ensure that the
hemisphere indicator is set to N or E.
The USGS GNIS (USA), NGA
GEOnet, and Getty Thesaurus databases
are comprehensive and authoritative, and include several search
options, but they do not provide information about time zones or
the observance of daylight saving time.
timeanddate.com.
The timeanddate.com
site has a smaller database, but is easy to use, and provides
the time zone and information about daylight saving time as well
as latitude and longitude for many locations inside and outside
the United States.
Location Map
Google Maps uses
Google™
Maps to provide road and terrain (topographic) maps as well
as satellite imagery for locations worldwide.
If either of Latitude or Longitude is nonzero, a Google Maps lookup will show a terrain map
centered on those coordinates.
If the “Specify” area already contains location
properties, and you want to look up a different location, be
careful to not simply enter a new name and click Go, because the map will be set to the
location given by the previous latitude and longitude rather
than that specified by the new name.
If a Name
is given and both Latitude and Longitude are zero, the lookup will search
for a location matching the name, and if a match is found, show
a map centered on that location.
If the name is blank and both the latitude and longitude are
zero, Google Maps shows a default Google
terrain map.
Google Maps works well in combination with
GeoNames Web Svc; you can find a
location’s properties using a GeoNames Web
Svc lookup, and then show a map of that location using a
Google Maps lookup. In addition to giving
a general preview of the terrain, the map can be helpful in
ensuring that a location selected from a large list of matches
to a GeoNames search is the location you
actually wanted.
Bing Maps uses Bing Maps to provide
location maps in manner similar to that of the Google
Maps option described above.
The location properties can also be entered manually; although this is usually not necessary, it may be the only choice for a location for which you have only the geographical coordinates, such as from a GPS reading.
The name is optional if Uses Daylight Time? is set to No. If Uses Daylight Time? is set to Yes, the country is required so that the correct rules for determining the beginning and end of daylight saving time can be used; if country is not specified, clicking Display or Print will result in an error message, and you will be directed to the name field to enter a country name. Although it seems silly, the place can be omitted, so that something like “, France” is acceptable. Unlike patterns passed to one of the online location-lookup services, country names and abbreviations are case sensitive.
For the United States and Canada, the state or province name (or its two-letter abbreviation) can be given instead of the country; for example, Hornitos, CA or Vancouver, BC. England, Scotland, Wales, Northern Ireland, and UK are recognized as United Kingdom; NZ is recognized as New Zealand.
If country is not recognized as a country, state, or province name, no DST rules will be available; if Uses Daylight Time? is set to Yes, a warning is given, and you can choose to continue or cancel the calculation. If you choose to continue, standard time is shown by default; see Daylight Saving Time for information on how to change this behavior.
Even if not required to perform the calculation, the name can be helpful in identifying the location to which the results apply, especially if results for several different user-specified locations are printed. Additionally, the name is passed to the weather service when seeking a forecast with the optional Weather feature.
The Elevation is the total distance above sea level, so if you are in a tall building or other man-made structure, you should increase the location’s elevation by the height of that structure.
Elevation can be given in either fixed or scientific (e.g., 8.2e3) notation. With fixed notation, a comma may be used to group digits; elevations greater than 9999 ft are automatically reformatted with a comma as a digit-group separator.
Elevation can be given in either feet or meters, depending on the unit selected under User Preferences; the appropriate unit is indicated after the text box.
The elevation of the horizon is not always the same as that for nearby terrain. For example, suppose you are in Colorado Springs, Colorado, and wish to know when morning sunlight will first reach nearby Pikes Peak, elevation 14,110 ft. Ideally, you would set the location to Pikes Peak, possibly getting the coordinates from the USGS GNIS or GeoNames, but the Elevation should be set to that of Pikes Peak in any event. Colorado Springs is at a nominal elevation of 6008 ft; however, the visible horizon from Pikes Peak is more than 130 miles to the east, at elevations from about 3800 ft to 4200 ft, so a height of 10,000 ft would be a reasonable nominal value. This is an extreme example; in many situations, the elevation of the horizon may be taken as that of nearby terrain. For example, if you were on Mount Davidson (elevation 928 ft) in San Francisco (nominal elevation 63 ft) and facing east, you could reasonably set the Elevation to 928 ft and the Height above Horizon to 865 ft. The greatest possible terrestrial value, approximately 28,940 ft, occurs on the summit of Mount Everest, at an azimuth of approximately 165° to the horizon along the Ganges; the distance is approximately 229 miles.
Height can be specified in either fixed or scientific (e.g., 6.5e3) notation. With fixed notation, a comma may be used to group digits; heights greater than 9999 ft are automatically reformatted with a comma as a digit-group separator. Height can be given in either feet or meters, depending on the unit selected under User Preferences; the appropriate unit is indicated after the text box.
The allowable range of values is 0 to the location’s elevation; values of a few feet or less have no significant effect on rise or set times, so that even a 7-foot observer can safely use the location’s elevation and the default height of zero.
Many of the national services cover only their own countries, but most of the others provide worldwide coverage. Some of the national services (France, Italy, and Mexico) do not have English-language versions.
Check the “Rise and Set Times” radio button to show Sun and Moon rise and set times for one or more dates.
A date offset in days is rounded to the nearest integer upon entry; with other units, the offset may be given as a decimal, though it is rounded down to the nearest integral number of days when performing the calculations. A value of 3.5 days is automatically changed to 4 days; an offset of 3.5 weeks is retained, but is rounded down to 24 days.
A date interval in days is rounded to the nearest integer upon entry; with other units, the interval may be given as a decimal. A value of 1.732 days is automatically changed to 2 days, but an interval of 1.732 weeks is acceptable (if silly). When the calculations are performed, each date calculated from the interval is rounded to the nearest integral date, so that specifying a non-integral date interval can result in uneven steps; this happens necessarily when the interval is in months (1/12 year) but usually makes little sense otherwise.
The calculator allows a total of 36,525 date calculations (100 years at a Date Interval of 1 day). Internet Explorer 8 and earlier versions perform the calculations very slowly compared with most other browsers, and are not recommended for date searches that span more than a few years.
Check the “Sun and Moon Positions” radio button to show Sun and Moon azimuths and altitudes between the two specified times. Rise and set times also will be shown for the specified date.
The start time can be an offset to the time of a selected event by entering a value, in minutes, in the text box to the left of the event box. The before/after drop-down box determines whether the start time is before or after the event. The allowable range of values for the offset is ±480 minutes; a decimal value is rounded to the nearest minute upon entry.
An explicit start time may be entered as hh:mm or in decimal hours; see the section DMS and HM Input for additional information. Allowable values are from 0 to 24 hours.
If a nonzero altitude has been specified for a rise or set event, the time of that event is the time the Sun or Moon crosses the specified altitude; if you want to show positions beginning slightly before and ending slightly after that altitude crossing, select that event for both start and end times, and also specify appropriate time offsets. For example, entering 5 and selecting before and Moonrise for the start time, and entering 5 and selecting after and Moonrise the end time would show positions between 5 minutes before and 5 minutes after the Moon crosses the specified altitude. Alternatively, you could note the time of altitude crossing and manually specify appropriate start and end times. In either case, you probably would want to select a time interval of 1 minute.
If a specified end time is less than the start time, it is assumed to apply to the next day.
If the default events Sunrise and Sunset are selected and neither occurs (as happens in polar regions in summer or winter), positions are shown hourly between 0:00 hours and 24:00 hours local time. Otherwise, if a specified start or end event does not occur, positions are not displayed. The behavior in either situation can be overridden by entering explicit start and end times and selecting a time interval.
Positioning the cursor over the label for any of the inputs displays a brief description of what the input is; with some browsers, the description also is displayed on the status line. Clicking on the label brings up the appropriate section on this page. Positioning the cursor over a major heading (e.g., “Location”) displays a similar message and link.
The Az/Alt Tool is described in detail in its reference.
The TPE Web app is described in more detail under Web Applications.
With some browsers, if the Use tabs for all pages preference is selected, and there is an existing tab for the page that a button opens, it may be necessary to manually select that tab.
With the default settings, the Sun/Moon Calculator will generate a table of Sun and Moon rise and set times that correspond to standard values. In many cases, this is all that is needed. However, there are situations for which these values may not be what is wanted. For a location in a valley bounded on the east and west by mountains, the Sun and Moon will appear above the eastern horizon later than the official time of rise, and will disappear below the western horizon earlier than the official times of set. In such situations, it may be more useful to know the times when the Sun and Moon cross the visible horizons.
Sometimes it also is desirable to find dates on which Sun or Moon rises or sets meet certain additional criteria, such as rising or setting near a landmark, the Moon having a certain phase at rise or set, the Moon rising or setting within a specified time of sunrise or sunset, or the Moon rising or setting when the Sun is within a certain range of altitudes.
The Sun/Moon Search Criteria form is shown in Figure 2; the criteria and
their effects are explained below.
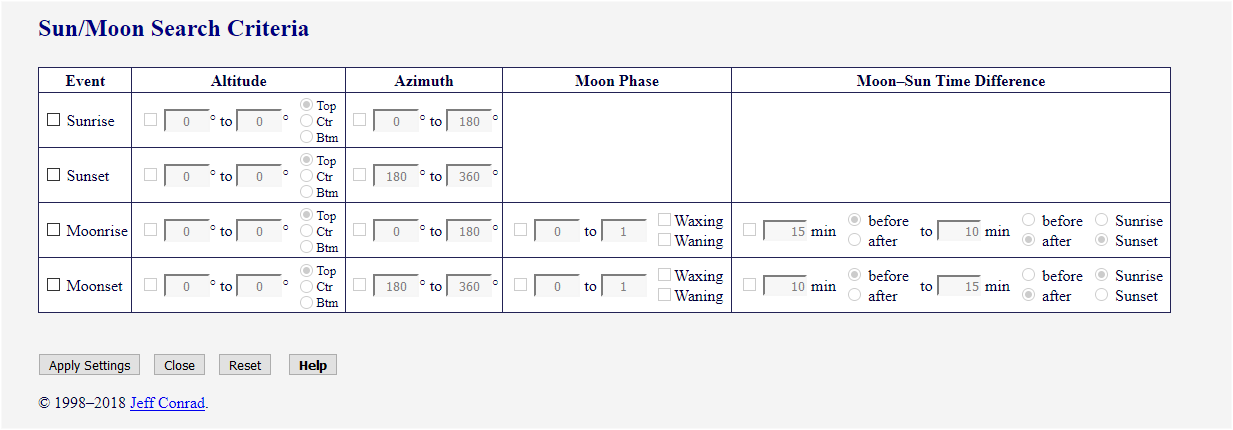
Figure 2. Sun/Moon Search Criteria Form
To the left of each Sun or Moon event is a checkbox; checking that box enables the row of inputs. Inputs in each column for an event can be enabled by checking the appropriate box, or simply by clicking on any of the inputs in that column. When the event checkbox is not checked, all other inputs for that event are disabled, and any values that were entered are ignored in calculations. When the checkbox at the left of a column is not checked, any values in that column for that event are ignored in calculations. This makes it easy to temporarily remove one or more criteria from a search, or to switch between two or more searches without having to re-enter the values later.
Altitude criteria are always applied; if the event box or the box at the left of the Altitude column is not checked, the default values of 0° and “Top” are used.
It seldom makes sense to specify criteria for the same body for both rise and set, and in most cases it is not allowed. There are two exceptions: a single altitude can be specified for two or more events, and a time-difference range can be specified for both moonrise and moonset.
A Sun altitude range given in combination with criteria for moonrise or
moonset is treated as part of the Moon criteria, requiring that the Moon
criteria be met while the Sun is within the specified range; it is
essentially equivalent to giving a Moon–
It seldom makes sense to specify a single value for other than altitude
or azimuth, and it almost never makes sense to specify a single value
for more than one criterion for the same body, because the odds of an
exact match in two or more criteria are very low.
If the Show Moon Semidiameter on
Sun/Moon Search Criteria form option on the User Preferences form is checked, an
additional column for specifying limits on the Moon’s semidiameter is displayed; the form then
appears as in Figure 3:
Figure 3. Sun/Moon Search Criteria Form with Moon Semidiameter
Semidiameter criteria are discussed under Moon
Semidiameter below.
By default, search criteria are applied only when searching for dates on
which the criteria are met.
If Apply search criteria to positions has
been selected on the User
Preferences form, the criteria are also applied when showing
Sun and Moon positions. This can be useful for showing only the times
on a given date for which the search criteria are met. It can also be
used to confirm that the dates found are valid; the date search employs
some approximations, and can occasionally show a date for which the
criteria are not met (although the difference will usually be very
slight).
Examining individual times is arguably a more foolproof approach, but it
isn’t perfect, and can miss dates on which the criteria are met
only very briefly. Moreover, it is “brute force,” and
accordingly is slow when searching wide ranges of dates. Because
position display is limited to 48 hours, speed is seldom an issue, but
because of this limitation, a position search cannot usually be used as
a substitute for a date search.
If a Moon–Sun time difference has been specified when applying
search criteria to positions, the time difference is that between the
time for which the Moon’s position is calculated and the time of
Sun rise or set, as specified.
When search criteria are applied to positions, the specified criteria
are shown at the top of the output. This can serve as a reminder that
this option has been set if certain times are mysteriously not
displayed.
A single value for altitude is taken as the time at which the body
crosses that altitude, i.e., “rise” or “set,”
and not a search criterion; to specify a search criterion, give an
altitude range. All other criteria should be ranges, because an exact
match to a single value is unlikely. Unless the ranges for all criteria
are very wide, the Time Interval should normally
be set to 1 minute to ensure that no times are
missed. Because of the way rise and set are implemented, it’s
usually also best to specify start and end times of 0 hours and 24 hours
local time.
Not all items below are shown by default; optionally displayed items are
enclosed in brackets (e.g., [Moon Semidiameter]).
Single Altitude
By convention, rise and set indicate
times when the Sun’s or Moon’s upper limb is on a
level horizon (i.e., the altitude of the top of the Sun’s
or Moon’s disk is zero). If the local horizon is not
level (e.g., near mountains), the times when the Sun or Moon
will rise above or set below those features can be substantially
different from the standard times of rise and set.
The Sun/Moon Calculator expands the definitions
of “rise” and “set” to allow
specifying an altitude other than zero; this can give the times
when the Sun or Moon actually will appear or disappear. For
example, if the western horizon is a mountain ridge at an
altitude of 9°, specifying set altitudes of 9° will give
the times when the Sun or Moon disappear below that ridge.
Any altitude can be given for the Sun; the Moon can be given any
altitude for which its upper limb is visible.
Properly, when a nonzero altitude is specified, the event is an
altitude crossing rather than a rise or set;
nonetheless, in the interest of simplicity, this document refers
to such an event as a “rise” or “set.” A
rise event is an altitude crossing that occurs when the
body’s altitude is increasing with time; similarly, a set
event is an altitude crossing that occurs when the body’s
altitude is decreasing with time. Either event can have the
time of altitude crossing be that of the body’s upper
limb, center, or lower limb.
Altitude Range
Sometimes it may be desired to find dates on which the Moon or
Sun passes through a region near certain natural or man-made
features; the easiest way to do this usually is to specify a
range of altitudes for Sun or Moon rise or set, in
combination with an azimuth or range of azimuths.
Specifying an Altitude or Altitude Range
The Altitude section contains two text
boxes: the first indicates the minimum altitude and the second
indicates the maximum altitude. Enter the desired altitude in
the first text box, either as dd:mm:ss or in decimal
degrees (see the section DMS and HM
Input for additional information). If the maximum
altitude is zero and a value greater than zero is entered for
the minimum altitude, the maximum altitude is set to the minimum
altitude. If desired, enter a greater value in the second text
box; if the minimum and maximum altitudes are the same, the
reported time of rise or set is the time that the body crosses
that altitude. Different altitudes or ranges of altitudes may
be given for sunrise, sunset, moonrise, and moonset. Allowable
values for Sun altitude are from −90° to 90°;
values for Moon altitude are from −3° to 90°,
although the minimum altitude for the Moon must also be at or
above the visible horizon. The Sun isn’t visible when its
altitude is below the horizon, but its position still influences
the brightness and color of the sky, and affects the visibility
of other celestial bodies. Specifying a negative altitude for
Sun rise or set in combination with a positive altitude for Moon
rise or set can be useful in finding dates for sighting or
photographing a thin lunar crescent.
To the right of each maximum-altitude text box are three radio
buttons, marked “Top”,
“Ctr”, and
“Btm”. By default, the
“Top” button is checked,
indicating that rise and set are when the Sun’s or
Moon’s upper limb crosses the specified altitude. To show
the times for the center of the Sun or Moon, select the
“Ctr” button; to show the
times for the lower limb, select the “Btm” button.
To the left of each minimum-altitude box is a checkbox; if it is
not checked, the altitude values are ignored; this allows a
nonzero altitude or an altitude range to be toggled on and off
without re-entering the values.
When an altitude range is specified, it usually is most useful
to have it apply to the center of the Sun or Moon; in
that case, the “Ctr” radio
button is automatically checked; this can be overridden if
desired by selecting the “Top”.
In some cases (e.g., having the setting Sun or Moon appear to
rest on the deck of the Golden Gate Bridge), you may want to
align the body’s lower limb with the specified
altitude; this can be done by selecting the “Btm” radio button.
For a Sun altitude less than zero, it seldom makes sense to
refer to the Sun’s upper limb (one possible exception is
when you are above the horizon and the Sun is visible at
negative altitudes). If a Sun rise or set altitude of less
than zero is specified without Moon criteria, the “Ctr” radio button automatically is
checked; this can be overridden if desired by selecting the
“Top” or “Btm” button. If a Sun altitude range
is given with Moon criteria, the alignment is always
Ctr”.
If an altitude range is given without other criteria (an
azimuth range for the same event, or a Moon event–
An exception is a sunrise or sunset altitude range given when
the Event box for one Moon event is also
checked; this requires that the Moon event occur while the Sun is
within the specified altitude range. The effect is similar to
giving only Moon–
The displayed value of Day Length is
the time the Sun is above the specified rise and set altitudes;
consequently, when the Sun rise or set altitude or both differ
significantly from zero, the Day Length usually is not
meaningful.
Sun Altitude Range with Moon Criteria
A sunrise or sunset altitude range can be given in combination
with criteria for the Moon to control the nature of the
foreground lighting and the appearance of the sky at the time of
Moon rise or set; the effect is similar to specifying a
Moon–
Limitations
The implementation of altitude range for the Sun or Moon alone
finds the time the body crosses the altitude that is the average
of the minimum and maximum altitudes. Because of this, very
large altitude ranges may not work as expected if the crossing
of the average altitude does not occur. For example, if you
were to specify a moonrise altitude range of 40° to 80°
with a moonrise azimuth range of 0° to 180°, dates on
which the Moon did not reach an altitude of 60° would not be
selected, even if the Moon did reach the minimum altitude of
40°. This usually isn’t a problem
because—
This limitation does not apply to a Sun altitude range given
with criteria for the Moon, however. For example, if you wanted
Moon criteria apply when the Sun was always more than 12°
below the horizon, you could specify the Sun altitude range as
−90° to −12°.
A specified altitude refers to the apparent altitude
when the body is visible; if a specified altitude for the Sun is
below the visible horizon, it refers to the true
altitude. Because the apparent altitude includes atmospheric refraction, the reported
altitude undergoes a step change as the body crosses the visible
horizon. Because of the step change, there is a range of
reported altitudes that do not occur; at sea level, this range
is approximately −0.83° to −0.26° for the
center of the body. For the Sun, specifying a rise or set
altitude (or altitude limits) within that range results in an
error message when attempting to show times or positions.
Although the Sun/Moon Search Criteria
form allows a minimum altitude of −3° for the Moon,
the Sun/Moon Calculator also requires that the minimum altitude
for the Moon be at or above the visible horizon. Specifying an
altitude that is below the visible horizon results in an error
message when attempting to show times or positions.
Enter the desired minimum and maximum values in the appropriate
text boxes. If a range of altitudes also is given, the dates
selected are those on which the Sun or Moon passes through the
specified region of altitude and azimuth; if a single nonzero
altitude is given, the azimuth range applies at the time of
altitude crossing. The allowable range for rise and set azimuth
is 0° to 360°, although rise usually occurs between
0° and 180°, and set usually occurs between 180° and
360°. At extreme latitudes, rise and set do not always
straddle transit; the azimuth of rise can be greater than
180°, and the azimuth of set can be less than 180°. If
the box is not checked, the azimuth values are ignored, and no
azimuth checking is done; this allows an azimuth range to be
toggled on and off without re-entering the values.
The maximum and minimum azimuths can have the same value; for
example, you might want to have the Sun’s or Moon’s
azimuth exactly match that of a terrestrial feature. This
makes little sense unless a range of altitudes is also given;
occurrences of an exact match in both azimuth and altitude are
few and far between.
Specifying an azimuth or azimuth range makes little sense unless
a range of dates also is given. In most cases, it also makes
little sense to specify an azimuth range for more than one Sun
event and Moon event, and even specifying a Sun event and a Moon
event may be unduly restrictive.
A specified azimuth range is relative to either true north or
magnetic north, depending on which is selected for display. The
conversion between magnetic north and true north is based on the
magnetic declination at the middle of the search period.
Because magnetic declinations are not constant, it usually is
better to select azimuths relative to true north when performing
a search that extends over several years, especially if the
search period is far outside the period for which the magnetic
model is valid. Stated succinctly: for best results, select
azimuths relative to true north when search criteria include
azimuth ranges.
It sometimes may be useful to specify values for
related Sun and Moon events, to control the direction of the
foreground lighting as well as the position of the Moon, but
these are very restrictive criteria that should be given only
with very good reason.
You can require that the Moon be waxing
(e.g., first quarter) or waning (e.g., last
quarter) by checking the Waxing or Waning box. This criterion can also be
helpful with a nearly new moon, because it determines the side
of the Moon’s disk on which the thin crescent will appear;
for some compositions, this may be important.
If the box at the left of the column is not checked, the values
for phase range are ignored, no phase checking is done, and
waxing or waning requirements are not applied; this allows a
phase range to be toggled on and off without re-entering the
values.
The value of 0.284° occurs when the Moon is at zenith; the
greatest value at the horizon is about
0.279°—
Criteria for semidiameter are of limited value in most cases,
serving mainly to reject otherwise perfectly suitable dates, and
should be given only when there is a very specific requirement,
such as a nearly exact match to a previous image, or perhaps a
very precise alignment of the Moon with one or more terrestrial
features.
If “supermoons” are important to you, a range of
0.277° to 0.284° might be used to search for them; the
exact minimum value would of course depend on how
“super” you require the moon.
If the box at the left of the column is not checked, the values
for semidiameter range are ignored, and no semidiameter checking
is done; this allows a semidiameter range to be toggled on and
off without re-entering the values.
This column is not shown by default; to show it, check
Show Moon Semidiameter on
Sun/Moon Search Criteria form on the User Preferences form.
As an alternative, you can specify a
Sun altitude range within which
the specified Moon criteria must occur. The effect is similar
to giving a time difference, though the relationship between
time difference and Sun altitude varies with the geographic
latitude and the time of year.
When a Moon altitude range is given, the time difference between
Moon and Sun events is the difference between the time of the
Moon’s crossing of the average altitude for the Moon and
the time of Sun rise or set. For example, if it is desired to
have the Moon between 3° and 4° at sunset, the time
difference is that between the time when the Moon is at 3.5°
and the time of sunset.
Enter the desired minimum and maximum values in the appropriate
text boxes. Use the radio buttons to the right of each text
box, marked “before” and
“after,” determine whether
each specified time is before or after the Sun event. Use the
radio buttons at the far right, marked “Sunrise” and Sunset,” to determine the Sun event to
which the time difference applies. For example, the default
values for moonrise indicate a moonrise that occurs between
15 minutes before sunset and 10 minutes after sunset.
Allowable values for the minimum and maximum time difference are
±1440 minutes (±1 day), although giving a
value equivalent to more than an hour or so usually serves no
useful purpose.
The default time limits assume conventional rise and set when
the Moon’s upper limb crosses zero altitude, and assume
that the Moon would be photographed some time after rise or
before set, at an altitude greater than zero; for example, a
full moon rising 10 minutes before sunset might be
photographed at 5 minutes after sunset at an altitude of
3°.
For example, if you want to capture the peak of the pink sky
color for a full moon rise, you might specify the desired
altitude range and a time difference of 5 to 15 minutes after
sunset; to capture a darker sky with building lights turned on,
you might specify a time difference of 10 to 25 minutes after
sunset. You could use these criteria to examine the next year
for opportunities to photograph a full moon during evening
twilight, and then look for a suitable location for each
resulting date.
To find alignments for a new moon, select the Sunrise radio button, and reverse the times
with respect to before and after; in the preceding example, you
could specify a time range of 20 to 10 minutes before sunrise.
Because a new moon is considerably less bright than a full moon,
you might want to have a slightly darker sky; you could do this
by requiring that the alignment occur further before sunrise,
e.g, 45 to 25 minutes before.
If the box in the Moon–
Alternative: Sun Altitude Range
The brightness and nature of the twilight sky is determined by
the Sun’s altitude. The pink “Belt of Venus”
appears in the eastern sky at or shortly before sunset, and the
blue Earth shadow becomes prominent shortly thereafter, perhaps
peaking at a solar altitude of −2° to −3°.
At lower altitudes, the pink fades, and the boundary between the
blue and pink becomes less distinct. At a solar altitude of
−4° to −5°, the boundary is usually gone,
and the sky is completely blue (as well as quite dark).
The time required for the Sun to reach an
altitude—
For example, to find dates on which the center of a setting new
moon is at 2° when the Sun is between −5° and
−4°, specify 2° and “Ctr” for moonset altitude,
−5° and −4° for the sunset altitude range;
the “Ctr” radio button for
sunset is automatically selected.
For a latitude and season for which the end of civil twilight is
30 minutes after sunset, this would give approximately the
same results as a time difference of 20 minutes after
sunset to 25 minutes after sunset without a sunset altitude
range.
When a Sun altitude range is specified in combination with a
Moon azimuth range, the center of the Sun’s disk is always
used; the radio button at the right of the Altitude column is set to “Ctr” when the Apply
Settings button is clicked.
Time Difference or Sun Altitude—
Though the correspondence is not exact, a Moon–
Choosing the Proper Reference: Sunrise or Sunset
In effect, a Moon event–
Equivalently, giving a suitably narrow sunset altitude range for
moonrise essentially requires a full moon; giving a sunrise
altitude range essentially requires a new moon.
Giving altitude ranges for both sunrise and sunset in
combination with Moon criteria make little sense, and
accordingly, doing so is disallowed.
A time difference or Sun altitude range is less useful for a
quarter moon. As a general rule, the Moon at first quarter
rises at noon and sets at midnight (standard time); the reverse
is true for last quarter. The events are equally close to
sunrise and sunset, and it’s not clear which reference to
use. A better approach is to specify a phase range and require that the Moon be
waxing or waning (e.g., phase of 0.4–
All specified criteria are applied simultaneously, so that if more
criteria than necessary are given, there may be very few results. It
usually is better to begin with fairly broad criteria, and then refine
the search by narrowing the appropriate criteria. Specifying search
criteria other than altitude usually makes sense only when
the date interval is one day; if you give search criteria with a
different date interval, you will get a warning asking you if that is
really what you want.
When any criteria other than rise or set altitudes are specified for an
event, dates on which that event does not occur automatically fail to
meet the criteria, and are not displayed.
A blank entry or one that contains only spaces is replaced with the
default value; if the default is wanted for only one field, this is much
more convenient than resetting the entire form.
All criteria involve ranges of values; if a valid minimum value greater
than the current maximum value is entered, the maximum value is set to
the new minimum. Similarly, if a valid maximum value less than the
current minimum value is entered, the minimum is set to the new maximum.
Positioning the cursor over any row label or column heading displays a
brief description of what the option does. Clicking on the label or
heading brings up the appropriate section on this page.
For some items you select from a list of options; for others, you enter
a value. If you enter an invalid value (e.g., a Date
Interval of 0), the value will often be
changed to a reasonable valid value; you can either accept this value or
enter another valid value. In other cases, the field for which you have
entered an invalid value will be highlighted, and an error message will
be displayed below the field (with Firefox, you need to pass the cursor
over the highlighted field to display the message); the message will
explain why the value is invalid. If a particular field (e.g., Time Offset) requires values to be within a certain
range, that range will be indicated:
Please enter a valid value
With most browsers, you will need to correct the error before doing
anything else; with others, such as Firefox, you are not forced to
correct the error immediately but will be unable to perform a
calculation until you enter a valid value; when this happens on the Sun/Moon Search Criteria form, you will be unable to
save changes until the invalid entry is corrected.
Not all items are shown by default; optionally displayed items are
enclosed in brackets (e.g., [Astro Dawn]).
Set Sun and Moon Positions Date to date
is displayed. Clicking on the date sets the positions Date to
date.
An asterisk (‘*’) appended to the year indicates
daylight saving time. See the section Daylight Saving Time for additional
information on the implementation and its limitations.
If Apply search criteria to
positions has been selected on the User Preferences form, the Start Time and End
Time are set to 0 and 24 hours local time and the Time Interval is set to 1
minute to ensure that all times for which the Sun or Moon
meet the specified criteria are displayed. If you want
different values, they can be set manually on the main form.
If a nonzero rise altitude has been specified, the altitude is
shown below the column heading. If the time refers to the
Sun’s or Moon’s center or lower limb rather than the
upper limb, an asterisk (‘*’) is appended to the
column heading.
If a Sun altitude range has been given in combination with a
Moon azimuth range, it serves only to require that the Moon
criteria be met while the Sun is within the specified range; the
time of conventional sunrise is displayed.
If the absolute value of a location’s latitude is less
than the absolute value of the body’s maximum declination (about 23.5° for the Sun
and about 29° for the Moon), the body can transit to either
the north or the south. If the declination at transit is less
than the latitude, the transit is to the south; if the
declination is greater than the latitude, the transit is to the
north.
For latitudes between ±30°, the
direction of transit is indicated by an appended n or
s.
If a nonzero set altitude has been specified, the altitude is
shown below the column heading. If the time refers to the
Sun’s or Moon’s center or lower limb rather than the
upper limb, an asterisk (‘*’) is appended to the
column heading.
If a Sun altitude range has been given in combination with a
Moon azimuth range, it serves only to require that the Moon
criteria be met while the Sun is within the specified range; the
time of conventional sunset is displayed.
This column is displayed if a time-difference range has been
given, or a Sun altitude range has been given with Moon
criteria; it is also displayed when any other Moon search
criteria have been given if the Show
Moon–
If search criteria restricting phase at rise or set have been
given, a trailing plus sign (‘+’) indicates a waxing
moon, and a trailing minus sign (‘−’)
indicates a waning moon. If Always show
whether Moon is waxing or waning is selected on the User
Preferences form, this indicator will always be
appended.
This information is shown only if Show
thin lunar crescent visibility is selected on the User
Preferences form.
Set Sun and Moon Positions Time to time on date
is displayed. Clicking on the time sets the calculator to
“Sun and Moon Positions” and sets the positions Date
to date and the positions Time to time.
Because of the Moon’s orbit around the Earth, the Moon
rises, on average, 49 minutes later each day. Consequently, at
any latitude, there is one day each month on which the Moon does
not rise, another on which the Moon does not transit, and
another on which the Moon does not set. Such events are
indicated by a dash (‘—’). At extreme
latitudes, there may be many days on which the Moon neither
rises nor sets; such events are indicated in the same manner as
for the Sun.
A minus sign (‘−’) appended to a time
indicates that the event occurs on the previous day; an
appended plus sign (‘+’) indicates that the
event occurs on the next day. This happens only when times
are shown in Universal Time (UT).
An asterisk appended to Azimuth in the column heading
indicates that rise and set azimuths are relative to magnetic
north rather than true north.
If the default events Sunrise and Sunset are selected and neither occurs (as happens in
polar regions in summer or winter), positions are shown hourly between
0:00 hours and 24:00 hours local time. Otherwise, if a specified start
or end event does not occur, positions are not displayed. The behavior
in either situation can be overridden by entering explicit start and end
times and selecting a time interval.
When the cursor is positioned over the column heading for any of the
outputs, the cursor changes to a help-select pointer; clicking on the
column heading brings up the appropriate section on this page.
When the cursor is positioned over the location name, the cursor changes to
a hand pointer. Clicking on the location name sets that location as the
selected location.
When printing rise and set times, either portrait or landscape
orientation usually is suitable, although portrait orientation obviously
will fit more results on a single page. When printing Sun and Moon
positions calculated at the default 30-minute interval, portrait
orientation usually is required to fit the results on a single page;
however, fitting the output to the page width may require adjustment of
the font size. By default, the output font size is not fixed, so the
user can adjust it to the extent that the browser allows, but the
range of adjustment may not be sufficient for the output to fit the page
width in portrait mode.
With most current browsers, specifying a font size is usually
unnecessary, especially with landscape orientation, though in some cases
it may be necessary to check a Shrink To Fit Page
Width (or similar) box on the Page Setup dialog.
With most current browsers, saving with the browser’s “Save”
or “Save As” command will save the main form rather than the
results. To save the results as an HTML file, use the
“Save” button at the bottom of the results page. With
Microsoft Edge, Internet Explorer 11, and Vivaldi, the “Save
as” dialog may appear on the window or tab for the Sun/Moon
Calculator main form; with IE and Vivaldi, there may be no indication
(e.g., flashing tab, bold text in that tab) that a prompt is pending.
If the system has a PDF printer available, the results can be saved as a
PDF file by printing to that printer. The Adobe Acrobat browser Add-on
usually saves the main form.
Several links are provided at the top of the Sun/Moon Calculator main
form:
The User Preferences form, shown in Figure 4,
is opened by clicking the Preferences link at the top of the main form;
each item on the form is explained below.
Figure 4. User Preferences Form
Some browsers save results in the window’s history,
allowing results of different calculations to be examined by
scrolling through the history. In such cases, this option may
not be needed, avoiding the clutter that obtains from having
many windows or tabs.
Tabbed browsing can be convenient when it is necessary to
frequently switch among different pages; this usually is much
easier than moving different windows around. For example,
searching for dates that meet certain criteria and then
examining the positions on the resulting dates to find the best
possibilities can involve frequent switching among the main,
Sun/Moon Times, and Sun/Moon Positions windows.
However, there also are cases in which a new window
(“popup”) may be preferable, as with dialogs such as
the Sun/Moon Search Criteria and User Preferences. The default is to allow
these dialogs to open in new windows and to allow Times or
Positions results and Help windows to open in tabs when the
browser is set to choose how windows are opened. Sometimes it
also is helpful to have the Help in a separate window so that it
can be placed over the input form or results that it is
describing; checking this preference allows that to be done.
However, if the Help or Tutorial pages must be consulted
frequently, it may be easier to have them in tabs.
When performing searches that may result in examining Sun or
Moon positions on several different dates, it may be preferable
to have the results in tabs, and have the times and positions
results in separate tabs. This facilitates rapid switching
between the main, times, and positions windows, and also usually
preserves each times and positions result in the browser’s
history, making it easy to compare different results by using
the back and forward buttons. In that case, Use tabs for all pages should be
selected, which will automatically deselect this option.
Internet Explorer 7 and 8 choose how to open windows when the
selection for When a pop-up is encountered:
under Tools|Internet Options|Tabbed Browser
Settings is set to Let Internet Explorer
decide how pop-ups should open.
With Firefox 1.5 and later, the selection for New
pages should be opened in: under Tools|Options|Tabs is set to a
new tab. There is one slight additional complication: in
the URL about:config, the preference browser.link.open_newwindow.restriction must be
set to the default value of 2.
Selecting this preference with a browser that does not support
tabs causes new windows to be opened at a specific size; this
can be convenient when the main window is maximized.
When this preference is not selected with a browser
that supports tabs (and the browser is set to choose the manner
of opening), behavior when opening Help is not always intuitive.
With Firefox 2 and later, if a Help tab is already open, no
new tab is created, but the Help window is not brought to the
front, and there is no indication that anything has happened.
When clicking a label for which context-sensitive help is
available, that section is positioned at the topo of the Help
window, but again, there is no indication that anything has
happened. Behavior is similar with Internet Explorer 7 and 8,
but the tab for the Help window flashes.
When Help is opened from the Sun/Moon Search Criteria
or User Preferences dialogs,
behavior also varies depending on whether a Help window is
already open. With Firefox 2 and later, if a Help window is not
open, a new tab is opened in the popup window; with Internet
Explorer 7 and 8, a new small popup window is opened.
Internet Explorer and Firefox also allow the user to force all
windows to open either in new windows or in new tabs. If the
browser is set to force opening new windows, this preference
should be checked.
If this preference is changed, any existing tabs for results, Help,
or Tutorial pages should be closed to avoid unexpected behavior.
If a browser that supports tabs is set to force opening in new
tabs, this preference usually should be checked.
If this preference is changed, any existing windows for results, Help,
or Tutorial pages should be closed to avoid unexpected behavior.
A caution is given if the Start Date (or the Date when
calculating positions) is outside the magnetic model’s
range; results are usually reasonable if the date is close to
the period for which the model is valid, but even so, errors for
some locations can be considerable. Accuracy degrades as the
date moves further from this period, and the indicated magnetic
declinations eventually have little relation to reality.
Current DST rules are used regardless of the date. Because the
dates of rule changes have been different for almost every
country, no attempt is made to determine the ranges of valid
dates. Although the report will indicate that the DST rules are
for the specified year, if that year differs substantially from
the present, the rules may be meaningless.
Current DST rules are used regardless of the date. Because the
dates of rule changes have been different for almost every
country, no attempt is made to determine the ranges of valid
dates. Although the report will indicate that the DST start and
end dates are for the specified year, if that year differs
substantially from the present, the dates may be meaningless.
Showing magnetic declinations and daylight saving time rules and
dates requires extra calculations, and, accordingly, requires
additional time to generate the location listing. Unless you need
this information, it probably is best to leave these boxes
unchecked.
Universal Time is incompatible with daylight saving time; if
“Universal time (UT)” is selected, the status of
“Show daylight saving time” has no effect on the
display of time. The status does affect the adjustment
of start and end times when switching between local time and UT.
When switching between UT and a local-time format, the labels
for the start and end times on the main form change between
“UT” and “local time,” and the times are
converted and possibly reformatted.
For example, if the calculator is set to show daylight saving
time, and show Sun and Moon positions for a location in
California in September (Pacific Daylight Time,
UT − 7) for times between 13:00 and
26:00 UT, and the time format
is changed to “AM/PM,” the times will be shown on
the form as 06:00 am and 09:00 pm and the positions shown for times
between 6:00 AM and 9:00 PM local time.
Daylight saving time and Universal time are incompatible; if
the format is “Universal time (UT),” the status of
“Show daylight saving Time” has no effect on the
display of time. The status does affect the adjustment
of start and end times when switching between local time and UT.
The location’s magnetic declination is shown at the top of the
page; the value is for the Date if “Sun and Moon Positions”
is selected, or for the Start Date if “Rise and Set Times”
is selected. If rise and set times are calculated for more than one
date, magnetic declination is recalculated every 30 days, and the value
shown at the top of the page is for the middle of the calculation
period. If the date is more than one year outside the range of time for
which the magnetic model is valid, the magnetic declination is not shown
unless azimuths are shown relative to magnetic north or conversions
between true and magnetic north are shown.
The data for the magnetic model used to calculate magnetic declinations
are valid for a limited time range, usually five years. If azimuth
display relative to magnetic north is selected and either the Start Date
or End Date (or the Date when calculating positions) is outside the
model’s range, a caution is given. If the caution is ignored, the
calculator will dutifully calculate magnetic declinations, but the
values may be significantly in error for dates substantially outside the
model’s range. The best response to such a caution is to display
azimuths relative to true north by deselecting this option.
A caution is included in the output if either the Start Date or End Date
(or the Date when calculating positions) is outside magnetic
model’s range.
Generally, showing azimuths relative to magnetic north makes little
sense if the calculation period extends over many years. This is
especially true if azimuths are given as search
criteria, because magnetic declinations change over time, while the
azimuths given as search criteria are static.
Any user-specified values for elevation or height are converted if the
units are changed.
This option is disabled by default. When showing rise and set
times at the default interval of one day, it is usually obvious
whether the Moon is waxing or waning; when performing searches,
however, results may be dates that are separated by months or
even years, so there are no adjacent values for reference, and
it sometimes can be helpful to have this information. If this
option is checked, it is retained across sessions, whereas
forcing display by checking a phase box on the Sun/Moon Search Criteria form affects only the
current session.
Some pairs of inputs on the main form are mutually exclusive;
when one is selected, the other is inactive. For example, when
calculating Sun and Moon rise and set times, if End Date is selected, Date
Offset is deselected and inactive. Similarly, when
calculating Sun and Moon positions, if a time value is selected,
giving the start or end time relative to a Sun or Moon event is
deselected and inactive. The disabled inputs make it more
obvious which inputs are active in the calculation but require
that the appropriate radio button be clicked to reactivate a
disabled input or change its value; when inactive inputs are
enabled, the value of an inactive input can be changed and the
input made active simply by clicking on the input.
Without this option, entering values is slightly more work, but
it’s slightly easier to see which values are used in the
calculations.
This option has no effect on the inactive area of the
main form, for which all inputs are always disabled.
When rise and set calculations extend over a range of dates, the
conversion shown is for the middle of the calculation period;
because the Sun/Moon Calculator recalculates magnetic
declination every 30 days, the actual conversions used at the
beginning and end of the calculation period may differ from the
value shown.
A caution is given if the date for which the conversion is shown
is outside the magnetic model’s range. Although results
are usually reasonable if the date is only slightly out of
range, errors for some locations can still be considerable.
Accuracy degrades as the date moves further out of range, and
eventually the indicated conversion has little relation to
reality.
With some browsers, the range of adjustment is limited, and even
the smallest adjustable size may not fit on a printed page, and
better printed output is obtained by setting a fixed font size,
typically 9–
With other browsers (e.g., Firefox) better results are obtained
by leaving the font size unspecified and allowing the browser to
shrink the output to fit the page. See the section Printing and Saving Results for
additional information.
Positioning the cursor over the description after any checkbox displays
a brief description of what the option does. Clicking on the
description brings up the appropriate section on this page.
For a location well above sea level, light from a celestial body
passes through less atmosphere, and the refraction is slightly
less than that at sea level. The difference is greatest at the
horizon, and decreases with the body’s altitude. Even at
the horizon, the difference is slight, on the order of 0.15°
at an elevation of 10,000 ft, and rise and set times change
by a minute at most.
Elevated Observer
For an observer at a height substantially above the surrounding
terrain, the visible horizon has a negative apparent altitude.
When displaying Sun or Moon positions for an elevated observer,
the refraction is included if it would put the center of the
body above the visible horizon. Because of this, the
body’s reported altitude shows a step change as the body
crosses the visible horizon; again, however, the body’s
actual motion is uniform. Because of the step change, there is
a range of reported altitudes that do not occur; the range is
wider for an elevated observer than for an observer at ground
level. For example, with a location at an elevation of
4000 ft and an observer at 10,000 ft above that
location, the visible horizon is at an apparent altitude of
−1.64°; when a rising Sun or Moon crosses the visible
horizon, its reported altitude immediately increases from
−2.42° to −1.64°, so that it never has an
altitude between −2.42° and −1.64°.
In calculating refraction, the Sun/Moon Calculator assumes a
sea-level temperature of 10°C and a sea-level atmospheric
pressure of 1010 mbar; when the location’s elevation
is known, these values are adjusted for elevation.
When a nonzero observer’s height is specified, the dip of
the horizon is shown in the output.
Magnetic declinations change slowly over time; using a value
from an old topographic map can lead to significant errors.
Even with a current value, it is important to be aware of the
limitations of the magnetic model used to calculate magnetic
declinations. The accuracy typically is ½°, but it
does not account for local variations, which sometimes can be
several degrees.
When calculating rise and set times, the Sun/Moon Calculator
recalculates the magnetic declination every thirty days. The
value shown at the top of the results page is determined for a
date in the middle of the calculation period; if the period is
greater than six months, the date for which the magnetic
declination has been calculated is displayed. Magnetic
declination is not displayed if the middle of the calculation
period is more than one year outside the model’s valid
range unless azimuths are shown
relative to magnetic north or conversions between true and magnetic
north are shown; a caution is given if that date is outside
the model’s range.
See the Technical Notes for a
description of how the Sun/Moon Calculator’s determines
magnetic declinations.
Unlike most sources, the Sun/Moon Calculator gives the topocentric phase rather than the geocentric phase. In theory, this should
better correspond to what would be observed, but in most cases
the difference between geocentric and topocentric phase is
slight, on the order of a fraction of a percent. Because of the
topocentric viewpoint, the transition between waxing and waning
(and vice versa) can differ from the times of full or new
moon—
Semidiameter increases with altitude because the observer gets
slightly closer to the body, and at zenith, the
Earth–
If the absolute value of a location’s latitude is less
than the absolute value of the body’s maximum declination
(about 23.5° for the Sun and about 29° for the Moon),
the body can transit to either the north or the south. If the
declination at transit is less than the latitude, the transit is
to the south; if the declination is greater than the latitude,
the transit is to the north.
Because Earth’s rotation is not perfectly uniform, UT is
not a perfectly uniform time scale. International Atomic Time
(Temps Atomique International, or TAI), determined from atomic
clocks by the Bureau International de Poid et Measures in
Sèvres, France, is as uniform is as currently possible.
There actually are several versions of UT; one, Coordinated
Universal Time (UTC), is derived from TAI but is adjusted by the
periodic addition of leap seconds so that it differs from UT by
no more than 0.9 seconds, and from TAI by an integral number of
seconds. UTC is the official basis of civil timekeeping
throughout the world. In the United Kingdom, Greenwich Mean
Time (GMT) has meant UTC, but in navigation, the meaning has
been slightly different. Accordingly, UTC is preferred for
worldwide timekeeping.
For most practical purposes, including any times used or
calculated by the Sun/Moon Calculator, UT, UTC, and GMT are
interchangeable.
Values for latitude, longitude, altitude, and azimuth may entered in DMS
(degrees:minutes:seconds) format; values for times for which to
determine positions may be entered in HM (hours:minutes) format.
The degrees, minutes, and seconds components of a DMS value are
separated by a colon (‘:’) or one or more spaces; the hour
and minute components of an HM value are separated by a colon. The last
component may be a decimal number, so that values in almost any common
format may be entered directly. An angle may be entered as degrees,
minutes, and decimal seconds; degrees and decimal minutes; or decimal
degrees. For example, a latitude of 37°46′30″ may be
entered as 37:46:30, 37:46.5, or
37.775. Similarly, HM values may be entered in hours and
minutes or decimal hours. For example, the time 10:15 may be entered as
10:15 or 10.25; decimal values are rounded to the
nearest minute. Leading zeros are not required for nonzero minutes or
seconds components, so that 106:7:8 is equivalent to
106:07:08. However, if a value less than one degree is given
as DMS, or a value less than one hour is given as HM, a zero is required
in the degrees (or hours) position (e.g., 0:25:17 rather than
:25:17. A value less than one minute must include zeros in
the degrees and minute positions (e.g., 0:0:17).
Only one decimal DMS or HM component is allowed, and it must be the
last. For example, 37:46.5 and 37:46:30.2 are
acceptable but 37.7:3.6 or 37.7:4 are not.
Several additional DMS formats are recognized, allowing direct copying
and pasting from many geographical databases. Some characteristics of
these formats are
Because these symbols require extra typing, there hardly ever is any
reason to use them for manual entry; they are permitted to allow
easy copying and pasting from databases such as the US National
Geospace Intelligence Agency or GeoNames.
If seconds are given, degrees and minutes must also be given; e.g.,
37°46′30″ is fine but
37°30″ is invalid.
Times may be given in either 24-hour (e.g., 19:21) or AM/PM
(e.g., 7:21 pm) format, regardless of the output time
display format. Either format can use HM or decimal hours. In AM/PM
format the ‘m’ and the space between the time and
the AM/PM specifier are optional; thus 7:21 pm,
7:21pm, 7:21 p, and 7:21p all have
the same effect. A start time of 12 am is interpreted as midnight
at the beginning of the specified date; an end time of 12 am is
interpreted as midnight at the end of the specified date.
After entry, start and end times are reformatted in the style of the
output time display format, so that if Show time
as AM/PM is selected on the User Preferences form, a time value
entered as 14.25 will be reformatted as 2:15 pm.
The Sun/Moon Calculator automatically switches between standard and
daylight saving time (“Summer Time” in most locations
outside the United States) if the selected location uses daylight saving
time. The rules are current as of June 2018. For some countries,
especially outside North America and Europe, the rules change
frequently; in most cases, the Sun/Moon Calculator provides rules for
2009 and thereafter.
For years earlier than 1916, no DST rules are provided, and all times
are shown as standard time.
On the day of transition to daylight time, an asterisk is appended to
the date, although the times for events occurring before the transition
to daylight time are in standard time. On the day of transition from
daylight time, the date is shown without an appended asterisk, although
the times for events occurring before the transition are in daylight
saving time. On the latter day, the times for events occurring between
the transition time and one hour earlier are ambiguous, because these
times occur twice. Should this be of concern, the ambiguity can be
resolved by calculating positions between midnight and the transition
time.
If the location is indicated as using DST, but no DST rules are found
(e.g., coordinates are specified by the user and no country is specified
in the Name field), all times are shown as
standard time. This behavior can be changed, via the User Preferences form,
by selecting “Use US DST rules or their inverse” under Time Display. Current United States rules are then
used for daylight time for locations in the northern hemisphere; for
locations in the southern hemisphere, the beginning and end times
of DST are reversed. To always use standard time, uncheck
“Show daylight saving time” on the User Preferences form.
To have a user a user-specified location “indicated” as
using DST, set the value of “Uses Daylight Time?” to Yes. Locations in the internal database are hard coded
as using or not using DST; but a location in the internal database can
be copied to a user-specified location to view its properties by
clicking Copy Selected Location; if desired,
then set the value of “Uses Daylight Time?” to Yes.
DST rules have precedence over indication. If a location is indicated
as using DST but the corresponding rules indicate that DST is not used,
standard time is shown. If a location is not indicated as using DST,
the DST rules are not checked, and standard time is shown.
Standard time can be forced by setting the value of “Uses Daylight
Time?” to No, but it’s usually easier
to uncheck “Show daylight saving time” on the User Preferences form.
Most of the fields on the Sun/Moon Calculator main form and the Sun/Moon Search Criteria form can
be set when the program starts by passing parameters to the program.
The use of URL parameters is described in the URL Parameter Reference
At moderate latitudes, the rise and set times determined by the Sun/Moon
Calculator are within a minute of the correct values, and azimuths and
altitudes usually are within a tenth of a degree of the correct values.
The results usually are more than sufficient for planning photography
and other outdoor activity, and may suffice for many amateur
astronomical observations. However, the accuracy may not be sufficient
for navigation, precise surveying, or high-precision astronomical
observations such as stellar occultations.
Results usually are reasonable for latitudes between approximately
±82° (e.g., including Canada’s Quttinirpaaq National
Park in Nunavut), although the accuracy is slightly less than at lower
latitudes. Accuracy degrades rapidly within a few degrees of the poles,
however, and the values reported there should be used with caution.
North of the Arctic Circle or south of the Antarctic Circle, there is at
least one day each year on which the Sun does not rise, and another on
which it does not set. At extreme latitudes, there are extended periods
of light and dark. For example, in Alert, Nunavut, the Sun does not
rise between the middle of October and the end of February, and does not
set between the first week of April and the first week of September.
During the periods of transition between light and dark, the Sun’s
path may be almost parallel to the horizon, and a very slight error in
the Sun’s position can cause a significant error in the times of
rise or set; the situation is similar for the Moon. During these
periods, reported times for Sun rise or set, and particularly for Moon
rise or set, can be substantially in error, and in some cases, the
calculator may fail to detect a rise or set.
Of course, it should be kept in mind that for days on which the Sun or
Moon is almost on the horizon for the entire day, the concept of rise
and set is somewhat different from what it is at moderate latitudes.
Because of variations in atmospheric conditions, the actual times of
rise and set can differ from the nominal times by a minute or more,
even at moderate latitudes. At extreme latitudes, the differences can
be even greater. Consequently, calculating these times to a precision
of less than a minute makes little sense.
The United States Naval Observatory is the preeminent authority in the
United States for the positions of the Sun, Moon, and other celestial
bodies. The USNO Astronomical
Applications pages include a wealth of information about
astronomical phenomena, calendars, time, and other related subjects.
The USNO offers a number of publications, including the
Astronomical Almanac, and several software products. The
site includes many links to other sources of astronomical and
calendrical information.
The USNO AA Data
Services include several that are useful to photographers:
These services implement daylight saving time only for US locations, and
only for years 1967 and later.
Locations can be selected from a database of 22,000 cities and towns in
the United States; location properties can be specified for locations
not in the database. Obtaining the same basic data provided by the
Sun/Moon Calculator requires several steps, but the USNO data are
sometimes slightly more accurate and are unquestionably authoritative.
USNO AA Data Services can also provide the phases of the Moon, times of
twilight, the beginnings of seasons, and many other astronomical data.
In 2009, The Photographer’s Ephemeris
introduced the concept of Sun and Moon calculations integrated with a
map, showing rise and set azimuths of the Sun and Moon as well as the
azimuths at any given time. It also allowed determination of azimuth
and altitude of natural features, helping visualize the Sun and Moon in
relation to the landscape.
The original version was a desktop app; versions of TPE for mobile
devices were released later, and included additional features.
Several similar applications, including
PlanIt! for Photographers,
PhotoPills, and
Sun Surveyor,
are also available.
Most of the apps allow lookup of locations by name or coordinates, and
allow saving looked-up locations; saved locations can usually be
exported to and imported from files or other applications. Some apps
allow adjustment of looked-up elevations and allow specification of
heights of man-made structures; in some cases, saved locations can be
given various tags to facilitate later use.
Some of the apps provide much additional information about the Sun and Moon,
including twilight, “golden hour” and “blue
hour,” and features to assist in photographing the night sky.
Most also allow searches of altitude and azimuth ranges in which you
want the Sun or Moon to appear; the ranges can be specified in several
ways, and initial values can usually be automatically set from the
positions of pins on the map. Some apps include a simulated camera
viewfinder; some include additional tools for exposure and depth of
field.
The apps usually include user guides and numerous video tutorials.
Time spent reviewing these materials is time well spent.
The free
Photographer’s Ephemeris Web App
shows Sun and Moon rise and set times and rise and set
azimuths as well as the azimuths at any given time. It enables
determination of azimuth and altitude of natural features, but does not
include a search for Sun and Moon positions.
It allows saving looked-up locations, which can be exported to and
imported from KML
files; saved locations can be synchronized with versions of TPE running
on mobile devices. There is no provision for specifying heights of
man-made structures.
The Sun/Moon Calculator determines ecliptic coordinates of the Sun and
Moon using the formulas of Van
Flandern and Pulkkinen (1979), which are accurate to within one arc
minute, and in many cases much better. For most non-scientific
applications, this is more than sufficient. Essentially the same
accuracy applies to Sun and Moon azimuths and to true (uncorrected for
refraction) altitudes, but because of the variability in atmospheric
refraction, not to apparent altitudes. The effect of refraction on
apparent altitude is discussed further under the section below on
refraction.
Rise and set times are determined using an iterative algorithm similar
to that of Yallop, Hohenkerk, and
Bell (2013, 515, Eq. 12.11); accuracy degrades at extreme
latitudes, and in some cases this method may fail to detect a rise or
set. For extreme latitudes, Yallop, Hohenkerk, and Bell (2013, 516, Eq.
12.13) suggest “a more systematic approach,” which may be
incorporated in the method of Meeus (1991,
97–99). Other methods, such as described by Sinnott (1989) and Montenbruck and Pfleger (1999,
46–56), largely avoid the problem by using inverse interpolation
to find the time of altitude crossing, but do so at the cost of
increased computational overhead. As noted above, the
calculator’s results for any location in its database are usually
reasonable.
Formulas for positions of the Sun and Moon, especially the latter,
involve many terms of trigonometric functions, and consequently require
considerable computational overhead. When determining rise and set
times, Sun and Moon positions are calculated at 0h, 12h, and 24h local
time, and the positions for intermediate times determined from quadratic
interpolation of the calculated positions. Interpolation significantly
decreases program running time, with insignificant decrease in accuracy;
the change in positions is usually less than 0.005°, and the change
in rise and set times is usually less than a second. Because rise and
set times are rounded to the nearest minute, however, a difference of a
fraction of a second can occasionally change a displayed value by a
minute.
Sinnott (1989) used essentially the same
positional interpolation scheme but a different rise and set algorithm
(inverse interpolation). Meeus (1991) used a
similar rise and set algorithm but interpolated from positions
calculated on three successive midnights rather than over a single day.
When showing Sun and Moon positions, all positions, including those for
rise and set times, are calculated rather than interpolated. The time
required to compute positions even at one-minute intervals is
sufficiently short that there is little perceptible benefit from using
interpolation. Rarely, results from a search or from a multi-day
rise/set time calculation may differ very slightly from rise and set
times shown at the top of the results for position calculations for one
of those days; as mentioned, however, the differences are usually
insignificant
All searches begin by determining the times that the Sun or Moon crosses
a specified altitude (which can be the default of zero).
Searches involving azimuth or altitude ranges or combinations thereof
are implemented by computing the declinations that correspond to the
limiting paths that meet the azimuth and altitude criteria, finding the
time that the body crosses the midpoint of the specified altitude range,
and comparing its declination with the limiting values; essentially the
same approach was used by
di Cicco (1991) to determine
the date of Ansel Adams’s Moonrise, Hernandez,
New Mexico.
For almost any reasonable search, the Sun’s declination is nearly
constant, changing at most about 1′
(1 arc minute) per hour; however, the
Moon’s declination can change by almost 15′ per hour as it
crosses the equator, so there is some loss of accuracy in a search that
specifies a large azimuth or altitude range for the Moon.
If an azimuth range is given with a single altitude, only one
declination—
If a time range for Moon rise or set relative to Sun rise or set is
specified with a Moon altitude range, the times at which the Moon enters
and leaves the specified altitude and azimuth ranges are computed, and
the resulting time range is checked for overlap with the specified
time-difference range. Similarly, if a Sun altitude range is specified
with a Moon altitude range, the times the Sun is at the limiting
altitudes are computed, and the resulting time range is checked for
overlap with the time range for which the Moon is within the specified
limits.
The times at which the Sun and Moon are at the altitude and azimuth
limits are determined by computing the hour angles for those altitude
and azimuth crossings; as above, the declination used is that at the
time of the midpoint altitude crossing. For the Sun, the assumption of
constant declination has little effect on accuracy; for the Moon, the
declination can change in the course of passing through large ranges of
altitude and azimuth, resulting in a slight loss of accuracy. To
account for this, the calculated time ranges are slightly increased; a
consequence is that it is sometimes possible to get dates that slightly
fail to meet the time criteria. In most cases, specified limits are
somewhat arbitrary, so this is of little consequence. And the
inaccuracies are usually small.
The times at which a body crossed the specified azimuth and altitude
limits could be determined more accurately by using an iterative method
similar to that used to determine the times of rise and set, adjusting
the declination in the process. But in most cases, program running time
would increase significantly, often with little practical benefit in
finding dates on which the body is within the desired ranges.
As previously mentioned, if a single altitude is given in combination
with an azimuth range (and for the Moon, possibly also with a
time-difference range), no approximations are used.
To ensure that a good opportunity is not missed, the safest approach is
to specify slightly greater ranges than needed, and to examine each
resulting date to verify that it meets the specified criteria. Because
the search criteria are often somewhat arbitrary, even a date that
barely fails to meet the criteria may nonetheless prove perfectly
acceptable.
For a search involving the Sun or Moon alone to succeed, the crossing of
the midpoint of a specified altitude range must actually occur, and this
requirement may not be obvious. For example, a search giving a solar
altitude range of −90° to 0° would fail on a day on which
the Sun’s minimum altitude was greater than −45°. This
limitation does not apply to a Sun altitude range given with Moon
criteria; for example, a Sun altitude range of −18° to
−90° would work whether or not the Sun reached a minimum
altitude of −54°.
When the absolute value of a body’s declination is greater than
the absolute value of the location’s latitude, the same azimuth
occurs twice while the body is ascending or descending. In some cases,
there are two different time intervals for which the body is within the
specified azimuth limits; when this happens, the calculator uses the
time interval closest to the time of the midpoint altitude crossing.
Alternatively, a “brute force” approach could be employed,
examining Sun and Moon positions at small time intervals and comparing
them with all specified criteria; this approach was briefly described in
Callahan (1981). Computers were much slower
in 1981; computing Moon positions at five-minute intervals, the search
required several days. Unfortunately, some of the azimuth and altitude
limits were entered incorrectly, and the date determined for the taking
of Adams’s Moonrise was incorrect; the
speed of the algorithm may well have made additional checks infeasible.
Computers today are much faster, but the “brute force”
approach is still very computationally intensive. Even if time intervals
were very small, (e.g., a few minutes or less), a grazing pass through a
specified range of altitude and azimuth could be missed if it occurred
between calculation intervals, so there might not be any real
improvement in accuracy—
Such a “brute force” approach is used when applying search
criteria when showing Sun and Moon positions; because the time period is
limited to 48 hours, however, the computational overhead has minimal
effect.
When calculating positions, times are rounded to the nearest minute, so
positions may not be calculated at the exact times a body is at search
criteria limits. Consequently, it is possible for a date determined by a
date search to show no times that meet criteria; the disparity can also
be the result of approximations used in the date search. Unfortunately,
there is no single, foolproof method for performing a search.
A “supermoon” is a perigee–
There is no standard definition of “supermoon”; the term is
credited to astrologer Richard Nolle, who described it as “a new
or full moon which occurs with the Moon at or near (within 90% of) its
closest approach to Earth in a given orbit.” This description is a
bit vague, but Nolle (2011) goes on to somewhat
clarify it by example. Fred Espenak (“Mr. Eclipse”)
explains it clearly and succinctly.
With Nolle’s definition—
The Sun/Moon Calculator has no special provision for finding
“supermoons” according to Nolle’s criterion; it simply
allows searching for dates on which the Moon’s semidiameter is
within a specified range. A fixed value for semidiameter is usually
more useful for activities such as photography; dates of Nolle
“supermoons” can be found in Espenak (2015), but they may not coincide with
rise or set events.
The distances for Moon apogee and perigee given in the Glossary are
extreme values for the period 1900 to 2900, computed using the methods
of Meeus (1991, 325–
By convention, rise and set times are calculated assuming atmospheric
refraction at the horizon of 34′. But refraction decreases
rapidly with altitude, so the standard value cannot be used when a
nonzero altitude is specified.
Rigorous calculation of refraction requires numerical integration, and
the attendant computational overhead would be prohibitive for a scripted
application. In addition, the calculations depend on a specific
atmospheric temperature profile, such as that of the 1976 U.S. Standard
Atmosphere. On average, this is a reasonable assumption, but deviations
from this profile can cause refraction at the horizon to vary by as much
as ±0.32° (Schaefer and
Liller 1990), so the precision implied by rigorous calculations can
be misleading.
The calculator uses the empirical formula of Bennett (1982, formula H for
R′m) (described also in Meeus 1991, 102–103) to calculate
atmospheric refraction when determining rise and set times for altitudes
greater than or equal to zero. To provide a smooth transition between
the standard rise and set altitude of zero and a user-specified altitude
greater than zero, the calculator also uses Bennett’s formula at
zero altitude. At sea level, this gives a value of 34.5′, which
differs slightly from the standard value. Because variations in
atmospheric conditions can cause the actual refraction at the horizon to
vary by ±20′, the use of Bennett’s formula rather
than the standard value has little practical significance.
Refraction is adjusted for the decrease of atmospheric density with
elevation, using the 1976 US Standard Atmosphere as a model; because
of this, rise and set times and Sun and Moon positions shown by the
calculator may differ slightly from those given by other programs that
do not take atmospheric density into account. If comparison with
another program is desired, the adjustment for atmospheric density can
be eliminated by selecting “Specify:,” clicking the
Copy Selected Location button, and entering an
elevation of zero.
Bennett’s formula gives the refraction when the apparent altitude
is known; Sæmundsson (1986) made
empirical adjustments to the coefficients in Bennett’s formula to
give refraction from true altitude, which is what is needed when
displaying Sun and Moon positions. At sea level the results of the two
formulas are essentially interchangeable (i.e., when
Sæmundsson’s formula is used with a true altitude determined
with Bennett’s formula, the result is very nearly the same
apparent altitude that was initially used with Bennett’s formula).
When adjustment is made for atmospheric density, the interchangeability
is slightly less good at low altitudes. To avoid this problem, the
calculator uses an iterative application of Bennett’s formula for
altitudes between 0° and 5° if the observer’s elevation is
not zero. At greater altitudes, the difference between the two formulas
is insignificant regardless of elevation; for altitudes greater than
5°, the calculator uses Sæmundsson’s formula to minimize
computational overhead.
For an observer at a height above the location’s nominal
elevation, the calculator treats the curvature of a light ray as
constant, in a manner similar to that described in Young and Kattawar (1998,
3786–3787), when determining the dip of the horizon and the true
altitude of rise and set. Actual ray curvature varies with elevation;
the calculator uses the curvature for an elevation 1/3 of the way
between the low and high elevations involved, and results are generally
in good agreement with results of more rigorous calculations using
methods of Sweer (1938) and Auer and Standish (2000). The methods of
Auer and Standish are also described by Hohenkerk and Sinclair (1985).
Sweer’s methods are the basis for many of the tabular values in
Woolard and Clemence (1966, 215),
whose work in turn is cited in Yallop, Hohenkerk, and Bell (2013,
516).
For determining negative apparent altitudes after rise (or before set),
the calculator uses an approach similar to that of Cameron et al. (1963) (discussed also in
Woolard and Clemence 1966, 219).
For positive apparent altitudes, the refraction is determined using
Bennett’s and Sæmundsson’s formulas, and is based on
the air density at the observer’s elevation.
Dates of transition to and from daylight saving time are derived from
the IANA Time Zone
Database (“Olson/tz”). The implementation is more
simplistic than with the Olson model. Some predominantly Muslim
countries (e.g., Morocco) revert to standard time for Ramadan, and
return to DST at its conclusion, giving two transitions to and from DST.
Because the Sun/Moon Calculator allows only one transition each way per
year, DST may be shown to be in effect during Ramadan in such countries
when it is not.
North America and Europe change rules infrequently, but this is not true
for the rest of the world. The Sun/Moon Calculator recognizes many of
these changes, but for a more limited time period than the Olson model.
Rules for the US and Canada are implemented from the time DST was
standardized (1967 and 1974) into the foreseeable future; for years
prior to standardization, the first standard rules are used. The
earliest year for most other countries is 2009.
No DST rules are implemented for any country for any year prior to 1916.
The Sun/Moon Calculator DST rules are updated less frequently than the
IANA rules; the current rules are based on tzdata2018e.
Magnetic declinations are calculated using the World Magnetic Model
(WMM) produced by the US National
Oceanic and Atmospheric Administration’s National Geophysical
Data Center (NOAA/NGDC) and the British Geological Survey (BGS).
This model is used by the US Department of Defense, the UK Ministry of
Defence, the North Atlantic Treaty Organization (NATO), and the
International Hydrographic Organization (IHO).
The WMM characterizes only the portion of Earth’s magnetic
field generated by Earth’s fluid outer core. Although the outer
core generates over 95% of Earth’s magnetic field, there also are
contributions from Earth’s crust and upper mantle, and from
electric currents in the upper atmosphere and near-Earth space (Maus et al. 2010); those additional contributions
are essentially not represented. Accuracy is typically ½° or
better; however, the local magnetic field may sometimes exhibit spatial
and temporal declination anomalies of several degrees when compared with
the WMM (Quinn et al. 1995).
Spatial anomalies are produced by natural features such as mountain
ranges, ore deposits, ground struck by lightning, and geological faults,
and by man-made features such as trains and other large vehicles,
railroad tracks, power lines, reinforced concrete, and other features
that contain ferromagnetic materials; in many cases, these anomalies are
nearly impossible to predict.
More precise models (e.g., the Enhanced Magnetic Model
produced by the NOAA/NGDC) are available, but they typically entail code
size and computational overhead that are infeasible for a scripted
application such as the Sun/Moon Calculator. Moreover, even the
advanced models cannot account for local effects such as rebar within
concrete sidewalks or nearby structures.
The algorithm used for the calculations is derived from that developed
by John M. Quinn of the United States Geological Survey. The WMM and
associated software are currently supported by the US National Oceanic and Atmospheric
Administration’s National Geophysical
Data Center; online calculators and downloadable software for
Windows and Linux are available on the NOAA’s World Magnetic
Model page.
Calculated values of magnetic declination should be used with caution,
especially when precise directions to a natural or man-made feature are
needed. If the positions of the observer and the feature(s) of interest
are accurately known, estimates of direction(s) from the observer to the
feature(s) obtained from mapping software or geodetic calculations
are often better than those determined with a compass.
For millennia, many cultures have used the sighting of a new crescent
moon as the basis for their calendars. Although many modern lunar
calendars are calculated, some still rely on first sighting of a new
crescent moon to declare the start of a new month.
A thin lunar crescent can be difficult to observe; the relative ease of
observation is briefly described on HM Nautical Almanac Office’s
Moon Watch
web site.
Methods for predicting thin lunar crescent visibility have existed since
at least the time of the Babylonians. They have since become more
sophisticated, but even current methods are largely empirical.
Roughly, a new moon rises and sets with the Sun. Immediately after
sunset, the twilight sky is usually too bright to allow sighting a faint
crescent moon. As the Sun moves below the horizon, the sky brightness
decreases; however, as the Moon’s altitude decreases, its
brightness decreases because of atmospheric extinction—the
absorption and scattering of light by Earth’s atmosphere.
The optimal time for sighting, then, involves a tradeoff between these two
phenomena. The process is similar at sunrise.
Bruin (1977, 339–340) suggested an
optimal viewing condition based on estimates of sky and Moon brightness
and the minimum contrast required to distinguish one from the other;
Yallop (1998, 4) used this criterion to
propose optimal times for sighting.
For a morning observation, the optimal time is
tb = tmr
+ 5⁄9 (tsr − tmr),
where tb is the “best” time,
tmr is the time of moonrise, and
tsr is the time of sunrise.
For an evening observation, the optimal time is
where tss is the time of sunset, and
tms is the time of moonset.
The visibility of the thin lunar crescent is estimated from the altitude
difference between the Moon and Sun and the width of the crescent at the
optimal time for observation.
The result of the calculation is expressed as a parameter q;
the ranges of q correspond to
visibility codes ranging from “A”
(easily visible with the unaided eye) to “F” (not visible);
the process is described in Yallop
(1998, 11–13). The parameter q is calculated using a
polynomial fit to tabular data given in the 1996 Indian Astronomical Ephemeris:
q = [Δhm–s
− (11.8371 − 6.3226 W′
+ 0.7319 W′2
− 0.1018 W′3)] / 10,
where Δhm–s is the geocentric
Moon–Sun altitude difference in degrees and W′
is the topocentric width of the lunar crescent in minutes of arc.
This parameter is usually not meaningful at other than the optimal times
discussed above. Accordingly, visibility information is not displayed
when showing Sun and Moon positions.
Observations with which the calculated values of q were
compared were mostly from sea-level locations; accuracy likely decreases
with elevations above sea level and deviations from standard atmospheric
conditions.
The calculator displays lunar crescent visibility only when the
Moon’s phase is 0.15 or less. This is not a very thin crescent,
but this value is used so that results can be compared with all of the
recorded observations in Yallop (1998, 6–11).
Auer, Lawrence H., and E. Myles Standish. 2000.
Astronomical Refraction: Computation for All Zenith Angles.
Astronomical Journal 119, no. 5 (May):2472–2474.
Bennett, G.G. 1982. The Calculation of Astronomical Refraction in Marine Navigation.
Journal of Navigation 35:255–259.
Bruin, Frans. 1977.
The First Visibility of the Lunar Crescent.
Vistas of Astronomy 21:331–358.
Callahan, Sean. 1981. Short Takes: Countdown to Moonrise. American Photographer, January 1981: 30–31
Cameron, Winifred S., John H. Glenn, M. Scott Carpenter, and John A. O’Keefe. 1963.
Effect of Refraction on the Setting Sun as Seen from Space in Theory and Observation.
Astronomical Journal 68, no. 5 (June):348–351.
di Cicco, Dennis. 1991. Dating Ansel Adams’ Moonrise. Sky & Telescope, November 1991, 529–533.
Espenak, Fred. 2015. Full Moon at Perigee (Super Moon): 2001 to 2100.
http://astropixels.com/ephemeris/moon/fullperigee2001.html.
Accessed 24 November 2015.
Hohenkerk, C.Y., and A.T. Sinclair. 1985. The Computation of Angular
Atmospheric Refraction at Large Zenith Angles. HM Nautical Almanac Office
Technical Note No. 63.
Maus, Stefan, Susan Macmillan, Susan McLean, Brian Hamilton, Alan
Thomson, Manoj Nair, and Craig Rollins. 2010. The
US/UK World Magnetic Model for 2010–
Meeus, Jean. 1991.
Astronomical Algorithms.
Richmond, VA: Willmann-Bell. ISBN 0-943396-35-2
Montenbruck, Oliver, and Thomas Pfleger. 1999.
Astronomy on the Personal Computer, 4th ed.
Berlin: Springer-Verlag. ISBN 3-540-67221-4
Nolle, Richard. 2011. Supermoon: What It Is, What It Means.
http://www.astropro.com/features/articles/supermoon/.
Accessed 24 November 2015.
Quinn, John M., Rachel J. Coleman, Donald L. Shiel, and John M.
Nigro. 1995.
The Joint US/UK 1995 Epoch World Magnetic Model.
Stennis Space Center, MS: US Naval Oceanographic Office.
Sæmundsson, Þorsteinn. 1986.
Astronomical Refraction.
Sky & Telescope 72 (July):70.
Schaefer, Bradley E., and William Liller. 1990.
Refraction Near the Horizon.
Publications of the Astronomical Society of the Pacific
102, no. 653 (July):796–805.
Sinnott, Roger W. 1989.
Ups and Downs of the Moon.
Sky & Telescope.
July 1989, 78–80.
Sweer, John. 1938.
The Path of a Ray of Light Tangent to the Surface of the Earth.
Journal of the Optical Society of America
28 (September):327–329.
Van Flandern, T.C., and K.F. Pulkkinen. 1979.
Low-Precision Formulae for Planetary Positions.
Astrophysical Journal Supplement Series
41 (November):391–411.
Woolard, Edgar W., and Gerald M. Clemence. 1966.
Spherical Astronomy.
New York: Academic Press.
ISBN 978-0-12-395702-3
Yallop, Bernard D. 1998.
A Method for Predicting the First Sighting of the New Crescent Moon.
HMNAO Technical Note No. 69.
Taunton, Somerset, England: HM Nautical Almanac Office.
http://astro.ukho.gov.uk/download/NAOTN69.pdf.
Accessed 16 June 2019.
Yallop, Bernard D., Catherine Y. Hohenkerk, and Steven A. Bell. 2013.
Astronomical Phenomena in Explanatory Supplement to
the Astronomical Almanac, 3rd. ed. Ed. Sean E. Urban and
P. Kenneth Seidelmann. Mill Valley, CA: University Science Books.
ISBN 978-1-891389-85-6
Young, Andrew T., and George W. Kattawar. 1998.
Sunset Science. II. A Useful Diagram.
Applied Optics 37, No. 18 (June):3785–3792.
The Sun/Moon Calculator is copyright Jeff Conrad, and all rights remain
with the author. There are no restrictions on personal use; however,
any commercial use or posting on a website requires express permission
of the author. You are free to redistribute the Sun/Moon Calculator,
provided that all files are included without modification, including
this paragraph. For personal use, you may revise any of the files in
whatever manner you choose, though you may not claim copyright in any
such revisions; when you modify any files, you are, of course, on your
own. For convenience, all files, including commented versions of the
scripts, are available for download in a single
zipped file.
The Az/Alt Tool is also subject to the
Google Maps™ API Terms of Service, linked at the lower
right of the map. Because these Terms of Service require that the
application be on a publicly accessible website, you may not run the
tool as a local application; accordingly, it is not included in the
zipped file provided for download.
The Sun/Moon Calculator is provided in the hope that it may be useful,
but without any warranty of any kind, express or
implied, and you assume all risk of use.
© 1998–2025 Jeff Conrad
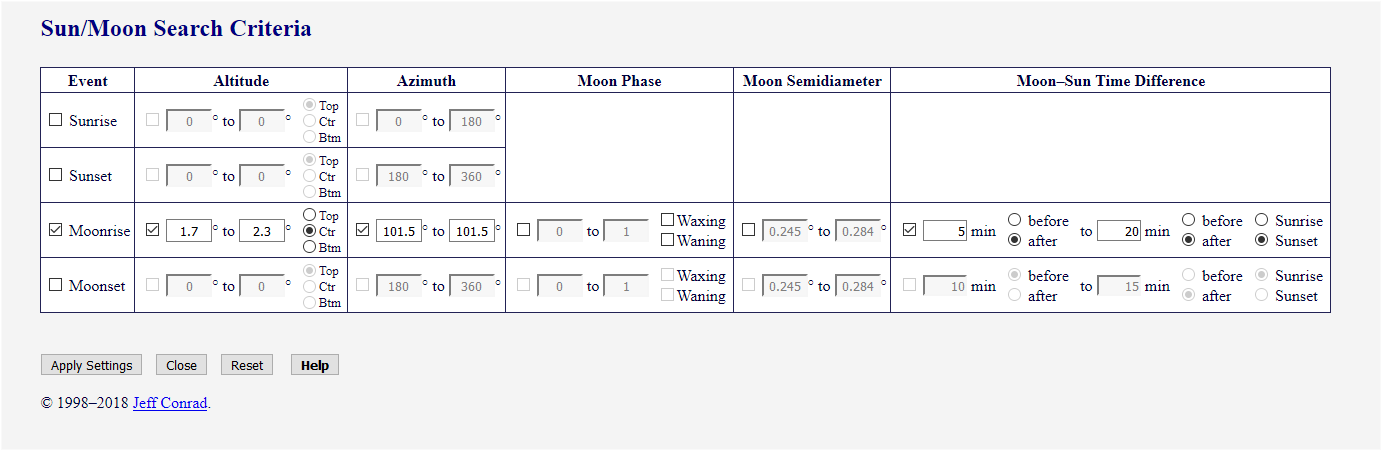
Applying Search Criteria when Showing Sun and Moon Positions
Specifying Search Criteria
Context-Sensitive Help for Sun/Moon Search Criteria
Sun/Moon Search Criteria Buttons
Data Entry and Validation
Range is 0 to 48 hours
Output
Rise and Set Times
Code
q range
Description
A
q > +0.216
Crescent easily visible to the naked eye
B
+0.216 ≥ q > −0.014
Crescent visible to the naked eye under perfect conditions
C
−0.014 ≥ q > −0.160
Binoculars or telescope may be needed to find crescent
D
−0.160 ≥ q > −0.232
Optical aid will be needed to find crescent
E
−0.232 ≥ q > −0.293
Crescent not visible with telescope
F
−0.293 ≥ q
Crescent not visible, below the Danjon limit
****
The Sun or Moon never sets
-----
The Sun or Moon never rises
/////
Astronomical, nautical, or civil twilight never ends;
the Sun’s altitude is always greater than
−18°, −12°, or −6°
===
Astronomical, nautical, or civil twilight never begins;
the Sun’s altitude is always less than
−18°, −12°, or −6°
—
No value for azimuth or time of rise, set, or
beginning or end of civil twilight, because the event does
not occur
Sun and Moon Positions
Times and Positions: Context-Sensitive Help
List Locations
Bottom-of-Page Buttons
The following buttons appear at the bottom of the page when displaying the results
of rise and set times, Sun and Moon positions, or location lists:
Printing and Saving Results
Top-of-Form Links
User Preferences

Window Behavior
Location Search
List Locations Report
Time Display
Azimuth Display
Twilight Display
Elevation and Height Units
Miscellaneous Options
User Preferences Buttons
Context-Sensitive help for User Preferences
Glossary
DMS and HM Input
Daylight Saving Time
URL Parameters
Limitations
Additional Resources
United States Naval Observatory
Applications for Mobile Devices
Web Applications
Technical Notes
Ecliptic Coordinates of the Sun and Moon
Rise and Set Times
Sun and Moon Positions
Using Sun/Moon Search Criteria
Azimuth and Altitude Ranges
Time-Difference and Sun Altitude Ranges
Search Criteria with Sun and Moon Positions
Semidiameter: “Supermoons”
Refraction
Refraction for an Elevated Observer
Daylight Saving Time
Magnetic Declination
Thin Crescent Visibility
Optimal Time for Sighting
Estimating Visibility
References
Legal