Guillotine Shutters
part
2: Determining
Shutter Speeds
© 2010 Bill Kumpf
for largeformatphotography.info
The guillotine
shutter offers a simple device to use with a barrel mount lens. It can be
quickly constructed from many materials in minimum time. For this article, a
report cover provided the material for one while scrap 1/8-inch plywood was
used for the second. This article provides a quick method to calculate the
effective shutter speed.
The guillotine
shutter uses a slot to pass across the lens. Being powered by gravity, the drop
blade is constantly accelerating as its drops. The leading edge of the shutter
opens the lens and the trailing edge closes it. The distance the edges fall
determines the drop times.
Calculating the drop time, T =
equals the square root of (2d/g) where d = drop (in), g=32 feet/sec2
_______________________________________
Time = Ã d x (
2 / ((32.17405 feet/sec2) x (12 inch / foot)))
Thus for an
initial drop of 1.75 inches and a slot with of 4.0 inches;
________________
The leading edge time, Tl = Ã (1.75 x 0.005180)
Tl = 0.0952 seconds
____________________
The trailing edge time, Tt = Ã (1.75 + 4.0)x 0.005180)
Tt =0.1726
For the exposure time T = Tt – Tli
T = 0.0774 seconds
To verify the
concept I meas
ured the shutter time using a
photoelectric eye and an oscilloscope. The leading edge activates the switch
while the trailing edge deactivates the switch. With the oscilloscope, the
activation time was measured.
Two series of
tests were conducted. The first used the same initial drop distance with
varying slot widths and the second used the same slot width with varying drop
distances.
The first
guillotine shutter provided shutters speeds of 1/15, 1/30, and 1/60 of a
second.
The slot width was set to give an
estimated exposure time:
|
Slot width (in) |
0.291 |
0.6645 |
1.4425 |
3.315 |
|
Dl= |
1.7850 |
1.7850 |
1.7850 |
1.7850 |
|
Tl = |
0.0962 |
0.0962 |
0.0962 |
0.0962 |
|
|
|
|
|
|
|
dt = |
2.0760 |
2.4495 |
3.2275 |
5.1000 |
|
Tt = |
0.1037 |
0.1126 |
0.1203 |
0.1625 |
|
Tl - Tt = |
0.0075 |
0.0165 |
0.0331 |
0.0664 |
|
|
|
|
|
|
|
Average Measured time |
||||
|
|
0.0074 |
0.0168 |
0.0336 |
0.067 |
|
% Difference |
1.89% |
-1.91% |
-1.38% |
-0.93% |
One
concern was vertical alignment. How far off the vertical axis could the shutter
be orientated before the friction would affect the drop rate? The drop rate was
checked at both 5¡ and 15¡. At 5¡ there was no measurable affect, while at 15¡
the shutter slowed approximately 5%. This will vary depending on the individual
shutter assembly and its internal friction.
|
|
Initial Drop |
0.1250 |
5.1250 |
10.1250 |
|
Vertical |
Time (sec) |
0.0479 |
0.0150 |
0.0106 |
|
15¡ Angle |
Time (sec) |
0.0506 |
0.0154 |
0.0110 |
|
|
|
|
|
|
|
|
Difference |
-0.0027 |
-0.0005 |
-0.0004 |
|
|
% |
5.64% |
3.01% |
4.15% |
The second series verified the
time distance function and to provide the bases of the following method to
determine shutter speed.
|
Drop |
1 |
3 |
5 |
7 |
9 |
11 |
|
Leading edge |
0.125 |
2.125 |
4.125 |
6.125 |
8.125 |
10.125 |
|
Tl |
0.0254 |
0.1049 |
0.1462 |
0.1781 |
0.2052 |
0.2290 |
|
|
|
|
|
|
|
|
|
Slot Width |
0.9955 |
0.9955 |
0.9955 |
0.9955 |
0.9955 |
0.9955 |
|
Trailing edge |
1.1205 |
3.1205 |
5.1205 |
7.1205 |
9.1205 |
11.1205 |
|
Tt |
0.0762 |
0.1271 |
0.1629 |
0.1921 |
0.2174 |
0.2400 |
|
|
|
|
|
|
|
|
|
Time (sec) |
0.0507 |
0.0222 |
0.0167 |
0.0139 |
0.0122 |
0.0110 |
|
|
|
|
|
|
|
|
|
Measured |
0.0479 |
0.02175 |
0.0164 |
0.01352 |
0.01176 |
0.0106 |
|
|
|
|
|
|
|
|
|
Difference |
0.0028 |
0.0005 |
0.0003 |
0.0004 |
0.0004 |
0.0004 |
|
|
-5.60% |
-2.12% |
-1.76% |
-2.95% |
-3.65% |
-3.59% |
Trailing Edge
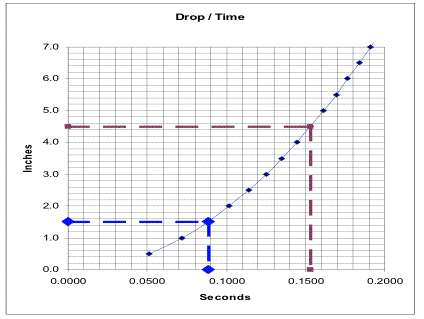
For example, if the shutter
design has a leading edge drop of 1 1/2 inches, on the chart find the 1.5 inch
line on the vertical axis, cross over to the line and read down to the drop
time of 0.0881 seconds. For the trailing edge, add the leading edge drop
distance and the shutter slot width and repeat the process. For an opening of 3
inches, the trailing drop distance is 4.5 inches. The time from the chart is
0.1527 seconds. The leading edge time minus the trailing edge time results in a
shutter speed of 0.0646 seconds. This is approximately 1/15 second.
For reference
|
f stop |
1/8 |
1/15 |
1/30 |
1/60 |
1/125 |
|
Time |
0.1250 |
0.0667 |
0.0333 |
0.0167 |
0.0080 |
Difference equals the shutter speed Trailing Edge Leading Edge
The constant acceleration also
varies the exposure during the shutter blade drop. This above process can be
applied to the drop / velocity chart to determine the variation in exposure.
The same process applied to the ÒDrop / VelocityÓ chart will estimate the
change in velocity. A doubling of velocity would result in 1 f/stop variation
in exposure. For our example above, the Leading Edge velocity is 34.03 in/ sec
and the Trailing edge velocity is 58.95 in/ sec. This is a 73.21% decrease in
exposure.
______________________________________
Velocity= Ã d
x 2 x (32.17405 feet/sec2 ) x (12 inch / foot)
Leading Edge
Hopefully this will help in
exploring the world of barrel lens.